Teil 1

Ton und Harmonie - die Ursuppe

Für Musik braucht man Töne. Aber was ist das, ein Ton? Welche Eigenschaft muss ein Geräusch haben, um ein Ton zu sein und eben nicht nur ein Geräusch? Töne müssen ein Musik­stück tragen können, z.B. als Teil einer Melodie. Dafür taugen Geräusche unter­schiedlich gut.

Hören wir uns das an. Zum Vergleich stehen vier Ideen für Musik­instrumente. Das erste Instrument ist ein normales Klavier. Beim zweiten schlägt der Spieler auf gedämpfte Becken. Beim dritten stößt er Champagner­gläser zusammen. Beim vierten schlägt er mit einem Boxhand­schuh gegen Sand­säcke. Vier Instrumente, die auf ganz verschiedenen Geräuschen beruhen. Nun der Versuch einer Melodie:

Klavier

---

Becken

---

Gläser

---

Boxsäcke

Mit dem Klavier und den Gläsern lässt sich spielen. Die Becken und die Boxsäcke dagegen können zwar einen Rhythmus produzieren, aber für eine Melodie sind sie nicht ernsthaft zu gebrauchen. Ihre Geräusche sind keine Töne.

Warum sind sie das nicht? Was fehlt ihnen?

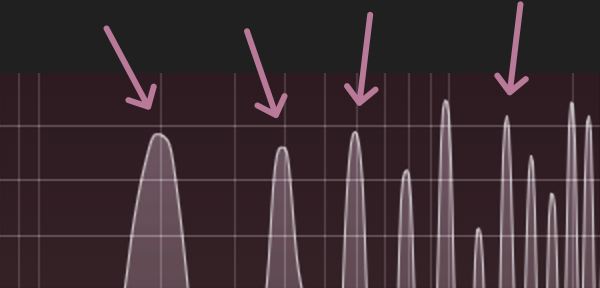
Geräusche sind aus Luft­schwingungen mit unter­schiedlichen Frequenzen zusammen­gesetzt. Diese Zusammen­setzung lässt sich analysieren. Folgende Diagramme schlüsseln die vier Geräusche nach Frequenzen auf, und zwar über das gesamte hörbare Spektrum zwischen 20 Hz (links) und 20 kHz (rechts). Je mehr eine Frequenz im Geräusch enthalten ist, umso höher ist die Kurve an dieser Stelle. Lässt sich eine Besonderheit erkennen, die die Töne von den Nicht-Tönen unter­scheidet?

Klaviersaite

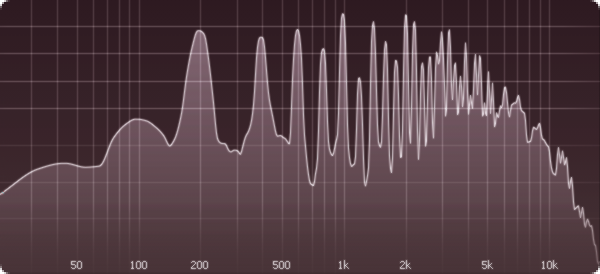
Becken

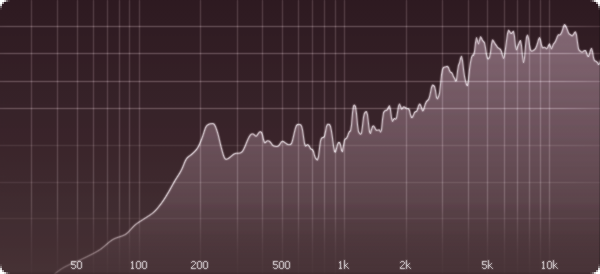
Gläser

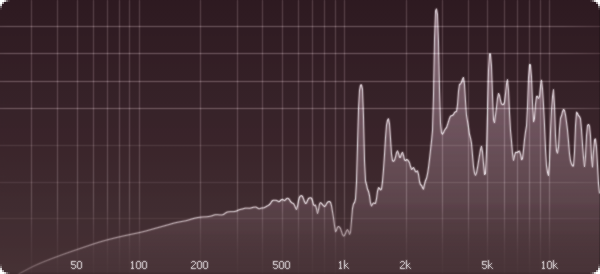
Boxsack

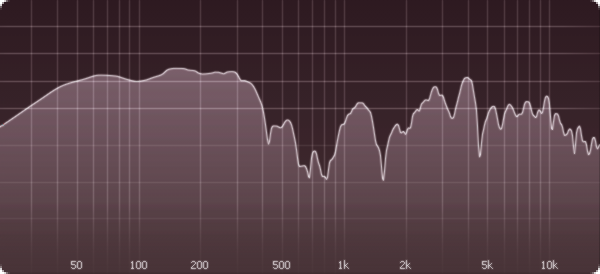
Die beiden Töne, also Klaviersaite und Gläser, zeigen auffällige Spitzen. Ein paar Frequenzen erheben sich weit über den Rest. Wenn das Ohr solche Spitzen braucht, um Töne zu hören, dann sind offenbar die Spitzen die eigentlichen Töne und der Rest nur Neben­geräusche. Für die Nicht-Töne dagegen zeigen die Diagramme eher kontinuierliche Kurven. Ein solches Geräusch ist quasi ein Brei von Frequenzen, aus dem für das Ohr keine heraus­stechen. Keine Frequenz, kein Ton. Töne sind Luft­schwingungen mit einer bestimmten Frequenz.

Das bedeutet dann aber, dass auch die beiden Geräusche, die als Töne funktionieren, in Wahrheit aus mehreren Tönen bestehen. Für die Klavier­saite z.B. sind im Spektrum etwa zwanzig Spitzen erkennbar. Anscheinend passen diese Töne so gut zusammen, dass sie als einer wahr­genommen werden.

Nachdem wir nun wissen, was Töne von Geräuschen abhebt, wäre noch interessant heraus­zufinden, wie sich hohe und tiefe Töne unter­scheiden. Welcher physikalische Umstand bestimmt über die Tonhöhe? Dazu suchen wir uns einen Ton mit wenigen Neben­geräuschen, spielen ihn in verschiedenen Höhen und analysieren jeweils das Frequenz­spektrum.

Also, drei Töne:

Die Spektren erweisen sich als folgende, in der gleichen Reihen­folge:

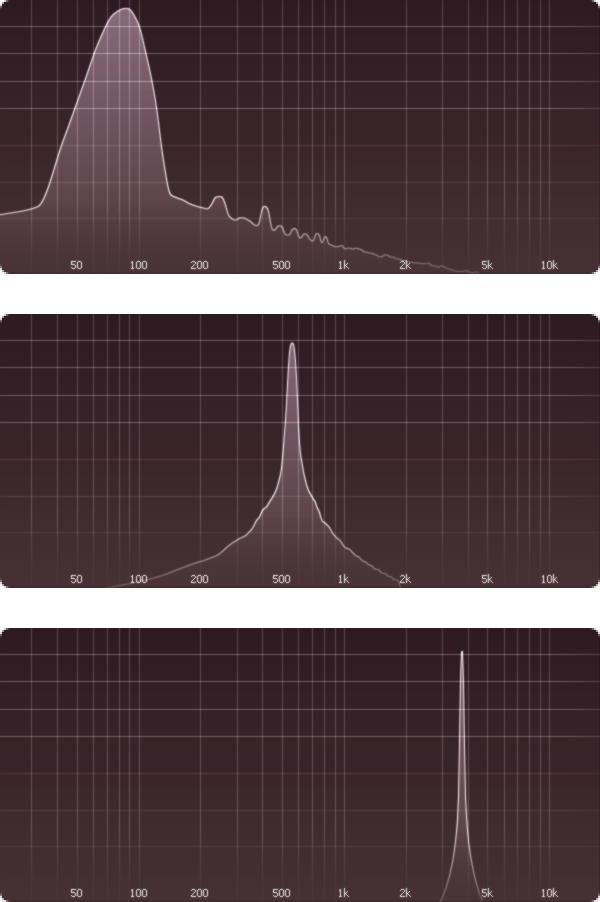
Erkenntnis: Die Tonhöhe hängt an der Frequenz der Schwingung. Langsame Schwingungen ergeben tiefe Töne, schnelle ergeben hohe. („Langsam“ ist hier natürlich relativ. Der tiefe Ton schwingt schon fast 100 Mal pro Sekunde. Der hohe allerdings fast 4000 Mal. Übrigens: Dass der tiefe Ton hier so viel breiter erscheint als der hohe, ist der begrenzten Auflösung der Spektral­analyse geschuldet. In der logarithmischen Darstellung werden die Mess­punkte bei den niedrigen Frequenzen weit auseinander­gezogen und ergeben nur grobe Hügel­landschaften. Eigentlich sind alle drei Töne Nadel­spitzen im Spektrum.)

Harmonie

Musik soll schön sein. Dazu gehört in der Regel, dass die Töne harmonieren. Wir wollen auch das in physikalischen Kategorien unter­suchen, und zwar mithilfe der eben gewonnenen Erkenntnis, dass Töne Frequenzen sind. Um Missver­ständnissen vorzubeugen: Wenn hier (oder allgemein in der Musik) von „Harmonie“ die Rede ist, dann geht es nicht direkt ums Gefallen. Mancher hat vielleicht ein Faible für Dissonanzen. Es geht um das objektive Phänomen von Einklang, Spannungs­armut, Konsonanz – und damit nur indirekt ums Gefallen, denn Einklang ist, was die meisten Menschen bevorzugen.

Was also lässt zwei Töne harmonieren? Ein Test soll das klären. Unten sind zwölf Knöpfe. Jeder lässt gleichzeitig zwei Streich­instrumente mit verschiedenen Tönen erklingen. Es handelt sich um spezielle Töne für diesen Test. Sie stammen nicht aus dem Vorrat, der üblicher­weise zum Musizieren verwendet wird. Die Frequenzen der Töne (in Hz) stehen auf dem Knopf. Die mittlere Tonhöhe ist überall die gleiche, der Durch­schnitt der beiden Frequenzen liegt immer bei 420 Hz. Welche der Paarungen klingen harmonisch? (Achtung: Im ersten Moment wirkt jede unharmonisch, weil man noch die vorherige im Ohr hat, die sich dazu immer schief verhält. Es geht aber darum, eine Paarung für sich zu bewerten.)

Wer keinen Unterschied wahr­zu­nehmen vermag und überall nur irgend­welche Streicher­klänge hört, für den hat zugehört vermutlich keinen großen Sinn. Nicht, dass er kein Freund der Musik sein kann, aber das bezieht sich dann offen­bar mehr auf Qualitäten wie Rhythmus, Klang, Ausschmückung und Ambiente. Hier liegen die Schwer­punkte bei den Tönen und Harmonien. Wer dafür kein Ohr hat, wird komplette Teile kaum nach­voll­ziehen können.

Es ist keine klare Zweiteilung in Harmonie und Scheußlichkeit, die sich ergibt, eher so etwas wie eine Rang­ordnung. Dabei fehlen die wirklichen Grenz­fälle schon, weil ich sie extra ausgespart habe, um die Sache an dieser Stelle nicht komplizierter zu machen als nötig. Bei manchen Paarungen ist die Harmonie sehr auffällig – heraus­ragend bei 280∶560, dort verschmelzen die beiden Töne fast schon zu einem. Ähnlich, wenn auch weniger ausgeprägt, verhält es sich bei 336∶504 und 360∶480. (Wer musikalisch vorbe­lastet ist, erkennt 336∶504 sofort als sogenannte Quinte. Diese Bezeichnungen kommen aber erst im dritten Teil ins Spiel.) Nochmals schwächer, aber durch­aus noch vorhanden ist die Harmonie bei 315∶525 und 373∶466. Die übrigen Zusammen­stellungen können kaum harmonisch genannt werden, das untere Ende der Hierarchie bilden gruselige Exemplare wie 265∶575 und 400∶440.

Mit etwas Sinn für Zahlen kann man bei den Paarungen 280∶560 und 360∶480 hellhörig werden, es handelt sich nämlich um die Verhältnisse 1∶2 und 3∶4. Tatsächlich weisen alle der harmonisch klingenden Paarungen ein einfaches ganz­zahliges Verhältnis auf – 336∶504 z.B. ist nichts anderes als 2∶3.

≈ 6∶13	1∶2	≈ 9∶17	5∶9
3∶5	≈ 7∶11	2∶3	≈ 7∶10
3∶4	4∶5	11∶13	10∶11

Offenbar liegt der Schlüssel zur Harmonie von Tönen im Verhältnis ihrer Frequenzen. Ein einfaches Verhältnis wie 3∶4 ist harmonisch, ein komplexes wie 7∶10 ist es nicht. Je kleiner die Zahlen in der Verhältnis­formel, desto größer die Harmonie. (Jeden­falls taugt das als grobe Richt­schnur. Hier sind schon Fälle dabei, wo es nicht ganz stimmt, z.B. ist 11∶13 fast schon auf der harmonischen Seite, weil es gar nicht als 11∶13 gehört wird, sondern als Annäherung an 6∶7.)

Dass sich das menschliche Gefühls­leben für Zahlen­verhältnisse interessiert, erstaunt im ersten Moment, ist aber durch Gewöhnung erklärbar. Man mag, was man kennt. Wir hatten oben einen flüchtigen Blick auf das Frequenz­spektrum einer Klavier­saite geworfen und dort eine Reihe von Spitzen ausgemacht. Sehen wir noch mal genauer hin. Wo liegen diese Spitzen?

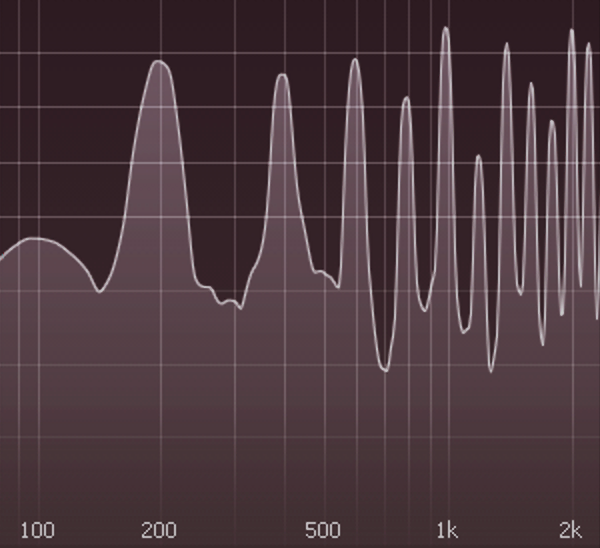
Die erste liegt bei 200 Hz, die folgenden bei Vielfachen davon: 400 Hz, 600 Hz, 800 Hz usw. Das ist eine typische Zusammen­setzung klarer natürlicher Klänge. Klang entsteht durch Schwingung. Meistens erlaubt die Physik an einer Stelle aber mehrere Schwingungen, die nicht einzeln, sondern nur als Komplex angeregt werden können. Hier beim Klavier schwingt eine Stahl­saite, also ein elastisches Gebilde zwischen zwei festen Endpunkten. Damit sind verschiedene Schwingungen möglich, und jede hat eine andere Frequenz.

×1	×2	×3	×7

Die Animation ist natürlich verlangsamt, und die Ausschläge sind stark überzeichnet. Die langsamste der Schwingungen ist die über die gesamte Länge, im Bild also die ganz linke. Die Frequenzen der übrigen Schwingungen, der sogenannten Obertöne, sind Vielfache davon, hier exemplarisch die Obertöne mit doppelter, dreifacher und sieben­facher Frequenz. Selbst die dreißig­fache Frequenz wäre bei einem tiefen Ton noch leise zu hören. All diese Schwingungen existieren gleich­zeitig und über­lagern sich.

Der Klang setzt sich aus den Frequenzen aller Schwingungen zusammen. Akustisch dominant sind dabei aber die niedrigen Vielfachen: ×1, ×2, ×3, ×4, ×5. Deren Frequenzen stehen zueinander in einfachen Verhältnissen. Deshalb sind natürliche Klänge von einfachen Frequenz­verhältnissen geprägt. Daran sind wir gewöhnt, das finden wir schön.