

|
| Zurück zu Teil |
Teil 2
Wenn Töne Frequenzen sind, dann bedeutet das: Es gibt unendlich viele verschiedene Töne. Das ganze hörbare Spektrum von 20 Hz bis 20 kHz ist ein Kontinuum von Tönen. Bekanntermaßen kommt in der Musik aber nur eine relativ kleine Auswahl an Tönen zum Einsatz. Selbst ein Klavier, dessen Töne drei Viertel des hörbaren Spektrums abdecken, kommt mit 88 Tasten aus. Das hat natürlich praktische Gründe. Für eine begrenzte Menge an Tönen kann eine übersichtliche Symbolschrift entwickelt werden, die der Interpret viel leichter ablesen kann als eine Liste von Frequenzangaben. Auch ist der Bau vieler Instrumente (wie eben eines Klaviers) nur möglich, weil die Anzahl der Töne, die in der Musik benutzt werden, überschaubar ist.
Die folgenden Betrachtungen gibt es in zwei Fassungen, einer langen und einer kurzen. Dies ist die kurze. Wer kein völliger Mathemuffel ist, dem sei die lange nahegelegt. Sie beschreibt das, was hier nur angedeutet ist: das Warum.
| Zur Langfassung geht es |
Die Auswahl an Tönen, mit der die westliche Musik seit Jahrhunderten arbeitet, wird chromatisches System genannt. Diese Auswahl ist sehr geschickt. Sie hat Qualitäten, die kein anderes System aufweist, das vergleichbar übersichtlich ist und mit gleichermaßen wenigen Tönen auskommt.
Der Tonvorrat ergibt sich dabei aus einem sehr einfachen Ansatz. Die Töne werden gleichmäßig über das Spektrum verteilt. Von einem Ton zum höheren Nachbarton wächst die Frequenz immer um den gleichen oder fast gleichen Faktor (letzteres bei alternativen Stimmungen). Der Faktor ist so gewählt, dass nach zwölffacher Anwendung exakt eine Verdoppelung erreicht ist.
Dreizehn aufeinanderfolgende Tasten auf einem Klavier, schwarze inbegriffen. Die Töne folgen einander im gleichen relativen Abstand. Der letzte Ton hat die doppelte Frequenz des ersten.

|
|
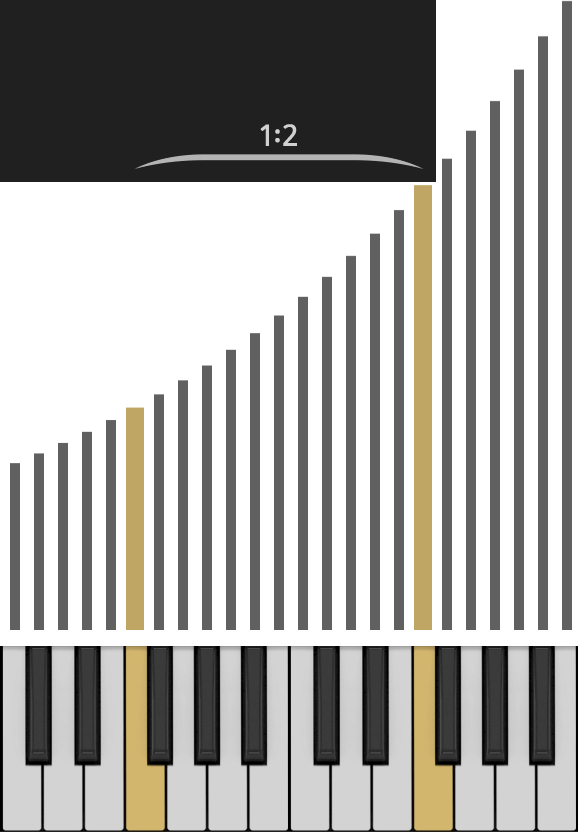
Die Längen der Balken über den Tasten stehen hier für die Frequenzen. Wegen der Art der Berechnung (konstanter Faktor) ist die Kurve exponentiell.
Die zentrale Rolle der Zahl Zwölf kann leicht zu falschen Vorstellungen führen. Die Zwölf ist ja eine alte Bekannte, sie erinnert an die Uhr und an die historischen Längeneinheiten mit zwölf Zoll pro Fuß. Sie ist eine Lieblingszahl des Homo Sapiens und wurde immer gerne für Unterteilungen verwendet. Die Zwölf im chromatischen System gehört nicht in diese Sammlung, sie hat einen ganz anderen Hintergrund. Sie ist nicht wirklich gewählt, sondern durch die Mathematik vorgegeben, und das auf eine sehr spezielle Art, die nur zufällig wieder bei der hübschen Zwölf landet. Die theoretischen Alternativen machen das deutlich: 19, 23, 31.
Es müssen zwölf Schritte sein, die zur Verdoppelung führen, denn die meisten anderen Teilungen leisten zwar gleichermaßen die Verdoppelung und machen so das Verhältnis 2∶1 verfügbar. Sie liefern aber nicht obendrein noch all die übrigen Frequenzverhältnisse, die harmonisch wichtig sind, nämlich 3∶2, 4∶3, 5∶3 und 5∶4. Die Teilung in zwölf Schritte tut das. Auf dem Weg zur Verdoppelung werden die anderen Verhältnisse mit eingesammelt, wenn auch nur als Annäherung.
| Schritte | Frequenz- verhältnis | etwa |
| 1 | 1,059 | |
| 2 | 1,122 | |
| 3 | 1,189 | 6∶5 (1,200) |
| 4 | 1,260 | 5∶4 (1,250) |
| 5 | 1,335 | 4∶3 (1,333) |
| 6 | 1,414 | |
| 7 | 1,498 | 3∶2 (1,500) |
| 8 | 1,587 | 8∶5 (1,600) |
| 9 | 1,682 | 5∶3 (1,667) |
| 10 | 1,782 | |
| 11 | 1,888 | |
| 12 | 2,000 | 2∶1 (2,000) |
Dass eine gute Annäherung genügt, wissen wir aus der Praxis. Keine reale Erscheinung enthält jemals absolut exakte Frequenzverhältnisse, auch Instrumente können unmöglich perfekt gestimmt sein, und doch hören wir Harmonie. Die Annäherungen von 5∶3 und 5∶4 sind ausreichend genau (< 1 % Abweichung), die von 3∶2 und 4∶3 sogar exzellent (ca. 0,1 %).
Aus Sicht der Harmonie lässt das chromatische System also kaum Wünsche offen. Zu jedem Ton sind auch alle Töne verfügbar, die gut mit ihm harmonieren, weil sie eins der harmonischen Frequenzverhältnisse aufweisen. Die kleinen Ungenauigkeiten sind für durchschnittliche Ohren nicht hörbar.
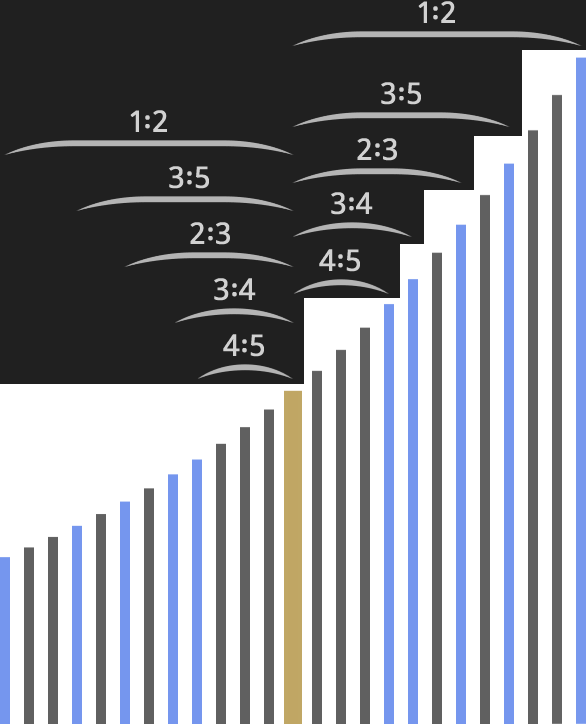
Klar ist an dieser Stelle auch, dass die Unterscheidung in große weiße und kleine schwarze Tasten auf Klavier, Keyboard & Co nur eine relativ geringe Bedeutung hat. Sicherlich wird das Musizieren dadurch leichter, aber es gibt keinen wesentlichen Unterschied zwischen den weißen und den schwarzen Tönen. Sie bilden gemeinsam eine gleichmäßige Reihe. Alles, was ein weißer Ton tut, kann in einem anderen Stück ein schwarzer tun und umgekehrt.
| Weiter zu Teil |