

|
| Zurück zu Teil |
Teil 3
|
Player einrichten
Alternative Playlist
|
Wir verfügen jetzt also über ein Sortiment von rund 100 Tönen, mit Bedacht ausgewählt aus dem Kontinuum der Frequenzen. Das chromatische System. Die Töne füllen das hörbare Spektrum absolut gleichmäßig aus. Benachbarte Töne haben überall das gleiche Frequenzverhältnis. Dieses Raster wird der Kosmos sein, in dem sich alles, was folgt, abspielt. Grafisch könnte man ihn so darstellen:
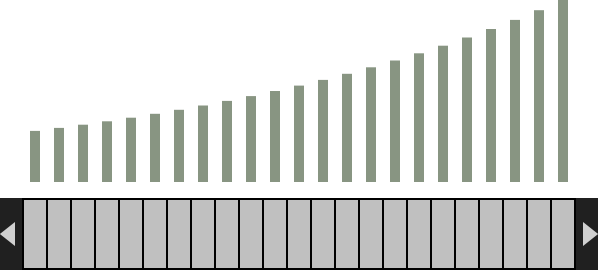
Die Geometrie aus einheitlich breiten Kästchen für die Töne des chromatischen Systems werden wir für grafische Darstellungen beibehalten. Gleiche geometrische Abstände zweier Töne bedeuten deshalb immer auch gleiche Frequenzverhältnisse – z.B. 2∶1 bei 12 Kästchen Abstand. Über den Kästchen sind hier ein letztes Mal die zugehörigen Frequenzen angedeutet. Zu sehen ist natürlich nur ein Ausschnitt des hörbaren Spektrums, aber es wird hier immer genügen, nur einen Ausschnitt zu betrachten.
Eine erste Struktur erhält die Landschaft der Töne durch den Brauch, bestimmte Töne trotz verschiedener Frequenzen als gleich zu betrachten, was sich auch im gleichen Namen niederschlägt. (Um das System hinter den Namen wird es erst später gehen, weil seine übrigen Aspekte weniger grundlegend sind. Hier ist zunächst nur die gleiche Benennung von Tönen interessant.)
Wir hatten festgestellt: Die größte harmonische Nähe, die zwischen zwei Tönen bestehen kann, ist das Frequenzverhältnis 2∶1. Solche Töne klingen trotz der unterschiedlichen Tonhöhe so ähnlich, dass sie als der gleiche Ton betrachtet werden und den gleichen Namen erhalten. Die Namensgleichheit pflanzt sich von 2∶1 zu 4∶1, 8∶1 usw. fort, sodass sich die gleich heißenden Töne über das gesamte hörbare Spektrum verteilen.
Diese Töne klingen irgendwie alle gleich. Deshalb heißen sie auch gleich, sie heißen alle G.

|
|
Wie wir wissen, entspricht ein Frequenzverhältnis von 2∶1 einem Abstand von 12 Tönen im chromatischen System, d.h. die Gs folgen einander im Abstand von 12 Tönen. Gleiches gilt für alle anderen Töne wie A, C oder E, was zur periodischen Wiederholung eines konstanten Musters führt.

Das bedeutet auch: Mit diesem Verständnis von Gleichheit kann es überhaupt nur 12 verschiedene Töne geben. Dass es am Ende doch etwas mehr als 12 Namen für Töne gibt, nämlich 17, liegt nur daran, dass manche Töne zwei Namen haben, wie wir noch sehen werden.
Beginn und Ende des wiederkehrenden Musters kann man sich natürlich an jeder Stelle denken, es steht nicht zwingend das A am Anfang.

So klug die Töne des chromatischen Systems gewählt sein mögen: der Vorrat hat immer noch beträchtliches Potenzial für Schiefes und Abenteuerliches, denn viele der Töne stehen eben doch in keinem harmonischen Verhältnis. Als Anschauung mag die Musik des Komponisten Arnold Schönberg dienen, der sich im frühen 20. Jahrhundert das gleichmäßige Verwenden aller Töne des Systems zum Prinzip gemacht hat.
Traditionell wird die Auswahl deshalb für ein einzelnes Musikstück noch weiter eingegrenzt, und zwar auf geschickte Art, sodass sich der Anteil an harmonischen Frequenzverhältnissen im Stück erhöht. Dafür gibt es verschiedene Muster, die sogenannten Tonleitern. Eine Tonleiter legt fest, welche der zwölf Töne einer Periode hauptsächlich verwendet werden sollen – meistens sind das sieben. Den übrigen Tönen – meistens also fünf – kommt allenfalls eine Nebenrolle im Stück zu, oft bleiben sie komplett außen vor.
Auch Tonleitern sind hier grafisch dargestellt. Die gewählten Töne erscheinen weiß, die ausgemusterten grau und verkürzt. Das könnte z.B. so aussehen:

oder so:

Das erinnert ein bisschen an die Tasten eines Klaviers, aber Achtung: in der Färbung liegt keine Zuordnung. Die Tonleiter lässt offen, auf welche Stelle im chromatischen System sie sich bezieht. Das kann in jedem Stück eine andere sein. Dagegen sind die Tasten des Klaviers natürlich mit festen Tönen verbunden. Deshalb können die Töne der Tonleiter auch auf schwarze Tasten des Klaviers fallen und weiße Tasten nicht zur Tonleiter gehören.
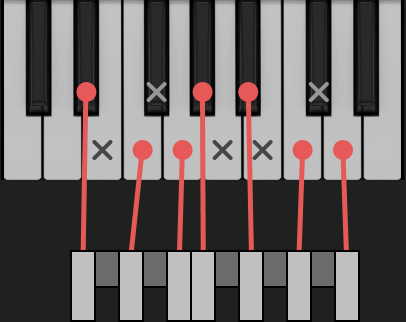
Neben der Eingrenzung übernimmt die Tonleiter gleich noch eine zweite Funktion. Die meisten Stücke haben einen Grundton, der eine tragende Rolle einnimmt. Man wählt die Periode, auf die sich die Tonleiter bezieht, immer so, dass sie mit dem Grundton als tiefstem Ton beginnt. Deshalb ist in der Angabe einer Tonleiter auch gleich die Information enthalten, welcher der Töne der Grundton ist: es ist der erste. Hier ist der Grundton zusätzlich farbig hervorgehoben.
Zwei Tonleitern sind mit großem Abstand die populärsten, sowohl in der klassischen Musik als auch im Pop:
 Dur
Dur
 Moll
Moll
Da sich eine Tonleiter auf die Töne einer Periode bezieht, wiederholt sie sich zusammen mit dieser. Beispiel Dur:
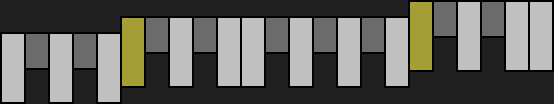
In der periodischen Wiederholung ergeben die Leitern von Dur und Moll das gleiche Muster, d.h. der einzige Unterschied liegt darin, welcher Ton des Musters zum Grundton gewählt wird. Das Muster heißt übrigens „diatonisch“, mit diesem Fachbegriff sei der Leser aber nicht weiter belästigt. Ggf. wird einfach vom Dur-/Moll-Muster die Rede sein.

Dur und Moll sind also stark verwandt, und für den Laien ist die Unterscheidung durchaus knifflig. Es geht das Gerücht, Dur klinge fröhlich und Moll traurig, aber das ist nicht mehr als eine Tendenz. Andere Eindrücke, z.B. die Klänge der Instrumente, wirken sich ebenfalls auf die Stimmung aus und können die feinen Unterschiede bei den Harmonien leicht überdecken. (Besonders wenn man bedenkt, dass sich die ganze Popmusik fast nur um den Klang dreht und viele Hörer kaum etwas anderes wahrzunehmen scheinen.)
Beispiel Dur

|
|
Beispiel Moll

|
|
Das einfachste Erkennungsmerkmal ist vermutlich der Schlussakkord, der im Allgemeinen der Grundakkord der Tonart ist und deshalb das gleiche Geschlecht hat. (Um Akkorde wird es in Teil 7 gehen.)
Aus welchem Vorrat an Tönen sich ein Stück bedienen kann, hängt sowohl von der Tonleiter als auch von ihrer Lage im chromatischen System ab, sprich: vom gewählten Grundton. Beide zusammen bilden die Tonart. Drei Beispiele:

|
 G-Dur
G-Dur
|
 A-Dur
A-Dur
|
 a-Moll
a-Moll
|
Da jeder der 12 Töne des chromatischen Systems als Grundton gewählt werden kann, gibt es 12 Dur- und 12 Moll-Tonarten.
Die Vorliebe für Tonleitern mit dem Muster von Dur und Moll besteht schon recht lange, deshalb bildet dieses Muster die Grundlage diverser Gebräuche in der Welt der Musik:
Es ist jetzt also an der Zeit, von unseren abstrakten Begriffen auf die üblichen, musikalischen zu wechseln. Beginnen wir mit dem wichtigsten. Um Abstände zwischen Tönen angeben zu können, wäre eine Einheit nützlich. Da das chromatische System regelmäßig ist, kann einfach der Abstand zwischen zwei direkt aufeinander folgenden Tönen als Einheit verwendet werden, denn alle anderen Abstände sind Vielfache davon. Es braucht für diesen Abstand nur einen Namen. Dazu wird die Situation aus Sicht der Dur-/Moll-Tonleiter betrachtet. Schreitet man auf der Tonleiter von einem Ton zum nächsten, dann wird dabei meistens (nämlich in fünf von sieben Fällen) ein Ton des chromatischen Systems übersprungen. Dieser typische Schritt auf der Tonleiter gilt als ganzer Ton. Ein Ganzton besteht aus zwei Schritten auf der chromatischen Leiter, die folglich Halbtöne genannt werden.
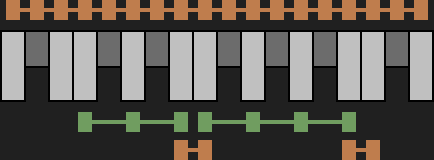
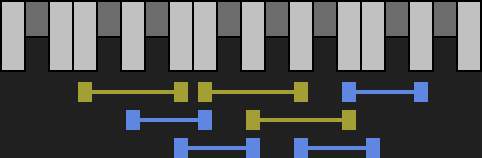
Ganzton (grün) und Halbton (orange). Der Halbton ist eine fundamentale Einheit in der Musik. Alle Abstände zwischen zwei Tönen lassen sich als Anzahl von Halbtönen angeben. Die Dur-/Moll-Tonleiter enthält fünf Ganzton- und zwei Halbtonschritte.
Abstände zwischen Tönen heißen in der Musik Intervalle und spielen eine große Rolle, denn ein bestimmter Abstand steht ja auch für ein bestimmtes Frequenzverhältnis und damit für eine bestimmte Art von Harmonie. Wegen dieser Bedeutung haben sich Namen für die verschiedenen Intervalle etabliert. Sie beruhen auf lateinischen Zahlwörtern. Die Namen beziehen sich aber nicht auf die Anzahl der Halbtonschritte, sondern maßgeblich ist einmal mehr die Dur-/Moll-Tonleiter.
Ein Beispiel. Ein Intervall von drei Schritten auf der Tonleiter heißt „Terz“ nach dem lateinischen Wort „tertius“ für das Dritte. Das klingt recht einfach, aber ganz so geradlinig ist es leider doch nicht. Erstens zählen Musiker auch den Ausgangston mit, deshalb ist eine Terz in Wahrheit nur zwei Schritte groß. Zweitens können zwei Schritte auf der Tonleiter verschiedene Intervalle ergeben, die Tonleiter ist ja unregelmäßig. Der Name „Terz“ allein ist nicht eindeutig. Es gibt kleine Terzen aus drei Halbtonschritten und große aus vier:
Insgesamt ergibt das Schema folgende Namen:
| Schritte auf der Tonleiter | Halbton- schritte | Name | ∶ |
| 1 | 1 (2×) | Kleine Sekunde | |
| 2 (5×) | Große Sekunde | ||
| 2 | 3 (4×) | Kleine Terz | 6∶5 |
| 4 (3×) | Große Terz | 5∶4 | |
| 3 | 5 (6×) | Quarte | 4∶3 |
| 6 (1×) | Tritonus | 7∶5 | |
| 4 | 6 (1×) | Tritonus | 7∶5 |
| 7 (6×) | Quinte | 3∶2 | |
| 5 | 8 (3×) | Kleine Sexte | 8∶5 |
| 9 (4×) | Große Sexte | 5∶3 | |
| 6 | 10 (5×) | Kleine Septime | |
| 11 (2×) | Große Septime | ||
| 7 | 12 | Oktave | 2∶1 |
Wir wissen nun also, wie unsere Periode aus 12 Halbtönen, die gleichzeitig ein Frequenzverhältnis von 2∶1 ist, offiziell heißt. Man durchschreitet sie auf einer siebenstufigen Tonleiter mit sieben Tönen, und der Musiker zählt noch den Ausgangston dazu. Deshalb „Oktave“ wegen des lateinischen Wortes „octavus“ für das Achte. Auch die Quinte und die beiden Terzen sind extrem wichtige Intervalle in der Musik und werden hier z.B. in Teil 6 wieder auftauchen, wenn es um Akkorde geht.
Jedes der Intervalle hat seinen eigenen typischen Klang, ein paar Beispiele:
Kleine Terz

|
|
Quinte

|
|
Oktave

|
|
Welches Intervall bilden A und D? Eine Quarte, natürlich. Aber nur, wenn man das D unmittelbar über dem A wählt. Nimmt man dagegen ein anderes D, nämlich das erste unter dem A, wird aus der Quarte eine Quinte. Quarte und Quinte sind also verwandt – durch bloßen Wechsel eines Tons in eine andere Oktave gehen sie ineinander über.
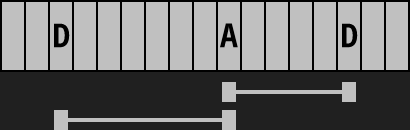
Solche Intervalle werden komplementär genannt. Komplementärintervalle ergänzen sich zu einer Oktave, d.h. die Summe ihrer Halbtonschritte ist 12, und das Produkt ihrer Frequenzverhältnisse ist 2.
Die klangliche Verwandtschaft komplementärer Intervalle durchkreuzt auch die allgemeine Regel, dass einfache Frequenzverhältnisse mehr Harmonie aufweisen als komplexe. So klingt z.B. die kleine Sexte (8∶5) harmonischer als der Tritonus (7∶5), denn sie komplementiert die große Terz (5∶4). Es deutet sich an, dass die Regel mit den kleinen Zahlen nur eine Faustregel ist, eine Annäherung an einen komplexeren Zusammenhang. Für unsere Zwecke wird sie aber reichen.
Es fehlen noch Namen für die Töne. Um konkrete Töne wird es hier bei zugehört selten gehen, trotzdem sei das Prinzip kurz erläutert. Ich werde aber nur auf die international übliche Namensgebung eingehen, mit der man spätestens bei der Arbeit mit Musiksoftware in Berührung kommt, und die auch etwas einfacher ist als die deutsche, die den Schreibfehler eines mittelalterlichen Mönchs mitschleift. (Dur und Moll nenne ich aber deutsch, was zu unüblichen Konstruktionen wie „B♭-Dur“ führt.)
Ausgangspunkt ist der Ton mit der Frequenz 440 Hz. Er heißt A. Wie schon dargelegt, heißen folglich die höheren Töne mit 880 Hz, 1760 Hz usw. sowie die tieferen mit 220 Hz, 110 Hz usw. ebenfalls A. Falls eine Unterscheidung nötig ist, werden die As durchnummeriert; der bei 440 Hz ist A4.
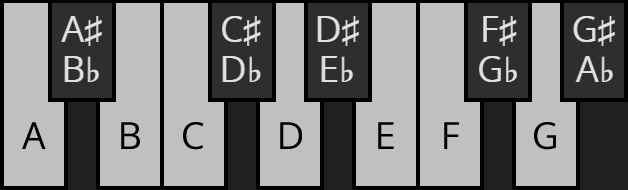
Die übrigen Töne erhalten ihre Namen, indem von A aus eine Molltonleiter abgeschritten wird. Der zweite Ton der Tonleiter (2 Halbtöne über A) ist B. Der dritte (3 Halbtöne über A) ist C usw. Die fünf Töne, die nicht zur Tonleiter gehören, werden nach einem der benachbarten Töne benannt, wobei es jeweils zwei Möglichkeiten gibt. Der Ton kann als oberer („erhöhter“) Nachbar des darunter liegenden Tons betrachtet werden, gekennzeichnet durch ein ♯ (gesprochen „Kreuz“). Oder er wird als unterer („verminderter“) Nachbar des darüber liegenden Tons gesehen, gekennzeichnet durch ein ♭ (gesprochen „Be“). Der Ton zwischen A und B hat also zwei Namen: A♯ und B♭.
| Weiter zu Teil |